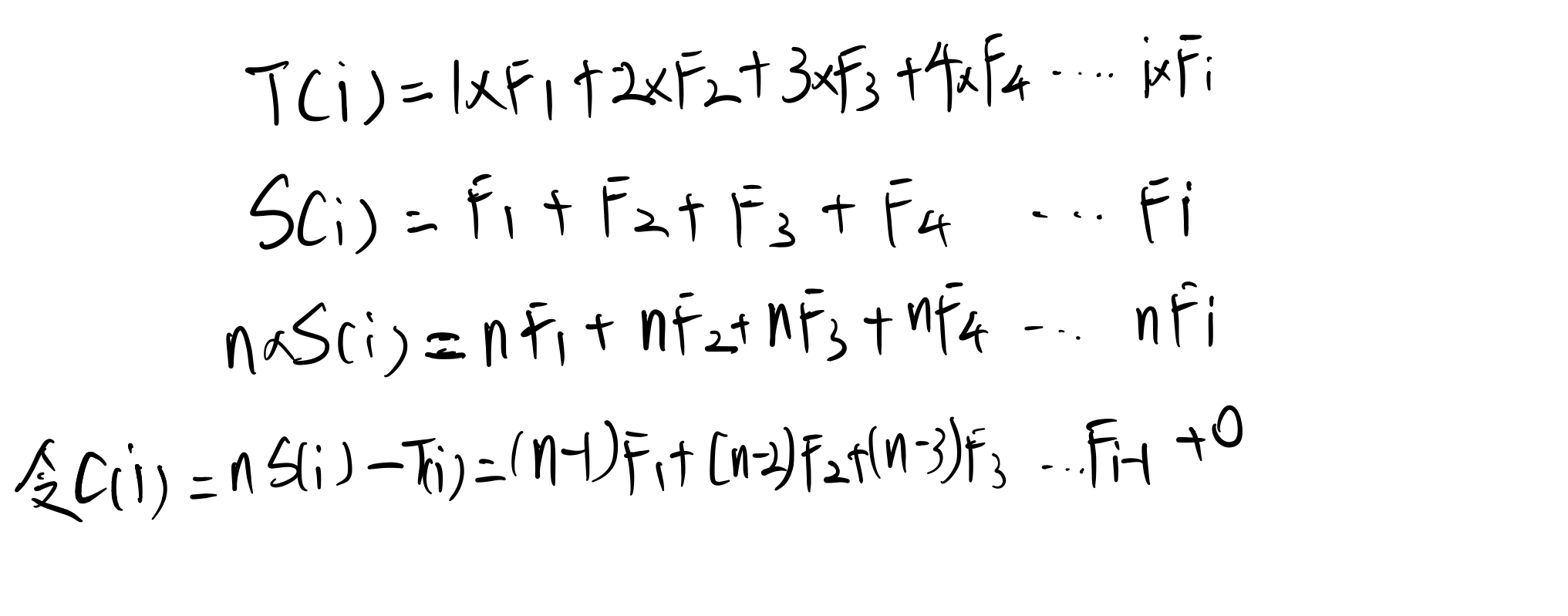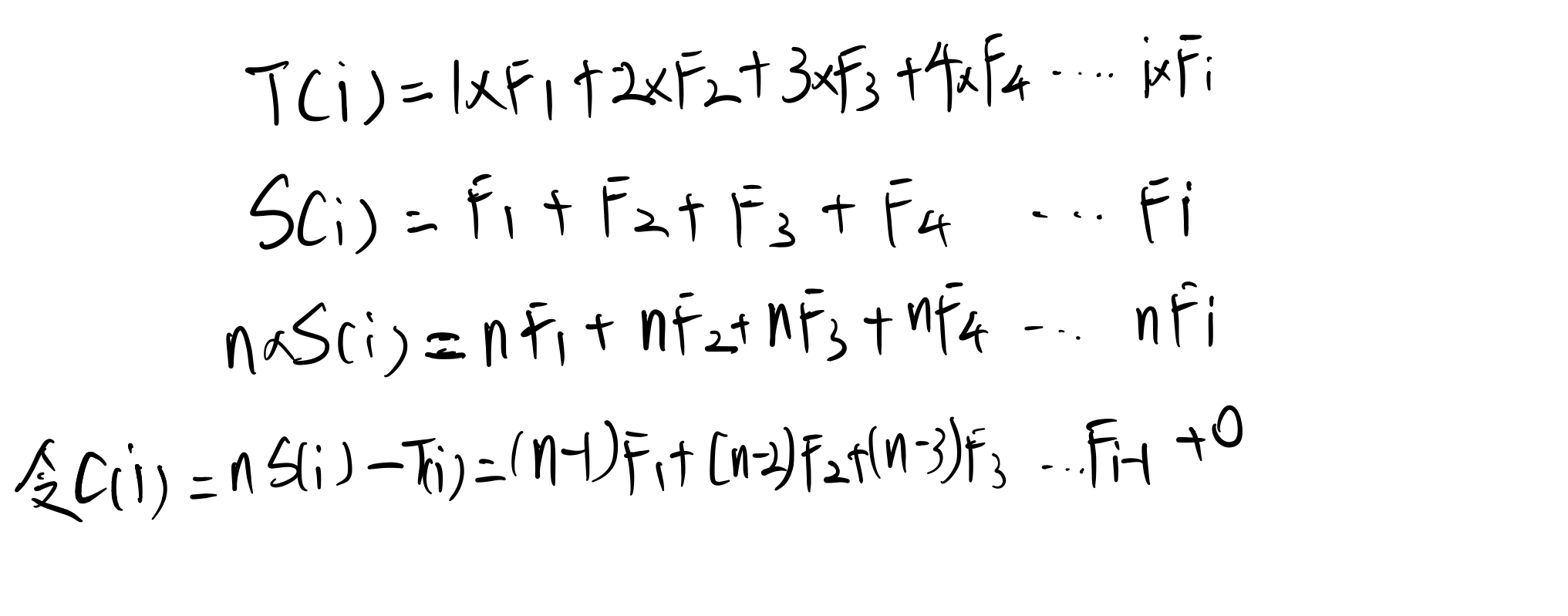1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
| #include<iostream>
#include<cstring>
#include<algorithm>
#define N 4
#define int long long
int n,m;
void mul(int a[][N],int b[][N],int c[][N])//矩阵乘法
{
int temp[N][N]={0};
for(int i=0; i<N; i++)
for(int j=0; j<N; j++)
for(int k=0; k<N; k++)
{
temp[i][j]+=b[i][k]*c[k][j]%m;
temp[i][j]%=m;
}
memcpy(a,temp,sizeof temp);
}
signed main()
{
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
std::cin>>n>>m;
int f[4][4]= {1,1,1,0};//f[i-1],f[i],s[i],c[i-1];
int k[4][4]=
{
{0,1,0,0},
{1,1,1,0},
{0,0,1,1},
{0,0,0,1},
};
n--;
int zz=n+1;
while(n)
{
if(n&1)
mul(f,f,k);//f=f*k;
n>>=1;
mul(k,k,k);//k=k*k;
}
std::cout<<((f[0][2]*zz%m-f[0][3]%m)%m+m)%m<<"\n";
}
|