Filling pools

发表于2022-06-02更新于2022-06-02

描述

Counting regionshttps://ac.nowcoder.com/acm/contest/33549/G

问n个点（n为奇数）每两个点之间都连一条直线,数多边形内的区域数。对1000000007取模

算法

G.png
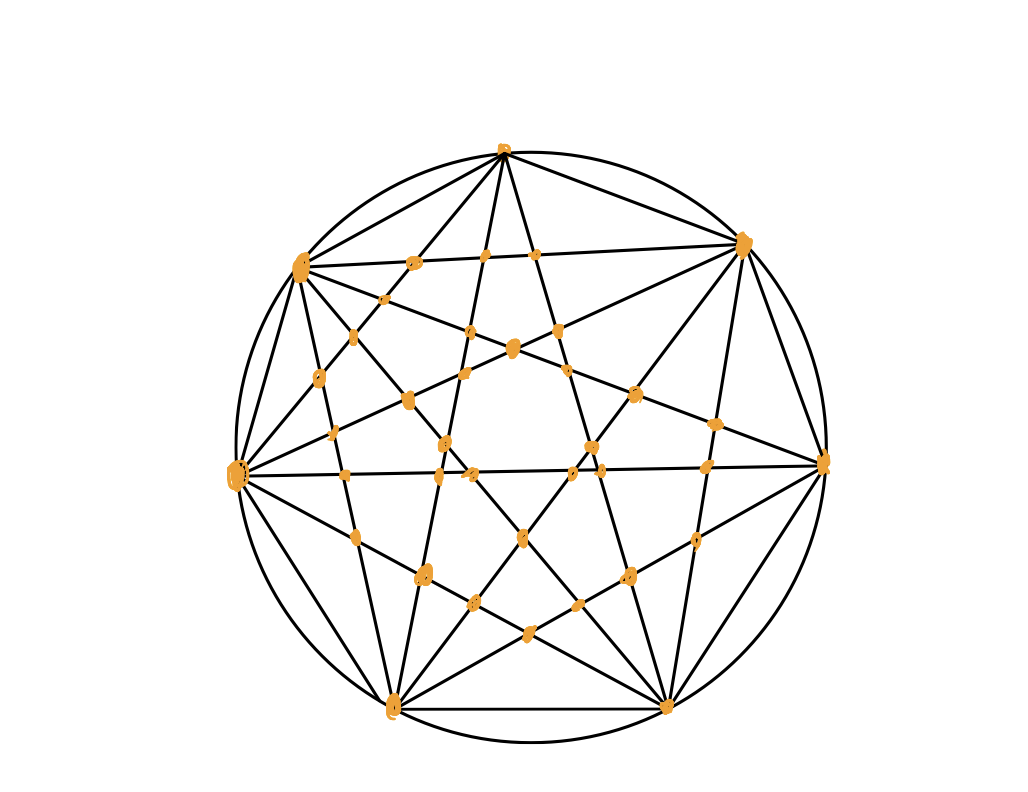
欧拉示性数公式：一个没有边的相交的图中V-E+F=2

点数-边的数量(包含弧)+分割区域+外围区域=2

本题中n个顶点 边相交了C(n,4)次 我们把每一条边都当成被分成若干份。

那这些小边的数量的就可以套用欧拉公式

如果 黄色是顶点 黑色是边

F=E-V+2

先求v（点的数量）:本身有n个顶点每两条直线相交得到一个点，一条直线有2个点 所以每四个顶点就会产生一个交点

V=C(n,4)+n;

然后求E(边的数量)： 每两个顶点会得到一条直线，每两条直线相交分把这两条线分成四份，交点。

E=C(n,2)+C(n,4)*2;

F=C(n,2)+C(n,4)*2-C(n,4)-n+2;

F=C(n,2)+C(n,4)-n+2;

由于欧拉公式里的F是算上外围区域的所以要减去1

F=C(n,2)+C(n,4)-n+1;

样例

1
输入：3 输出1

C++ 代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
#include<iostream>
#define int long long
#define mod  1000000007

int  qmi(int a,int b){
    int ans=1;
    a%=mod;
    while(b){
        if(b&1)ans=ans*a%mod;
        b>>=1;
        a=a*a%mod;
    }
    return ans;   
}
signed main(){
    int n;
   std:: cin>>n;
    int  cn2 =n*(n-1)%mod*qmi(2,mod-2);
    int cn4 = n*(n-1)%mod*(n-2)%mod*(n-3)%mod*qmi(24,mod-2);
    //cout<<cn2<<"   "<<cn4<<endl;
   int  ans = cn2 + cn4 - n + 1;
   std:: cout<<ans%mod<<"\n";
    
}