1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
| #pragma GCC optimize(2)
#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>
using LL = long long;
const int N = 1e5 + 10;
std::vector<std::vector<int>> g(N);
int in[N];
int n, m, cnt, root = 1;
int id[N], son[N], sz[N], depth[N], fa[N];
int nw[N], top[N];//新点的权值 以及每个重点的头
/*树链*/
void dfs(int v, int father) {
depth[v] = depth[father] + 1;
fa[v] = father;
sz[v] = 1;
for (int i: g[v]) {
if (i == father) continue;
dfs(i, v);
sz[v] += sz[i];
if (sz[i] > sz[son[v]])son[v] = i;
}
}
void dfs2(int v, int t) {
id[v] = ++cnt;
nw[cnt] = in[v];
top[v] = t;
if (!son[v])return;
dfs2(son[v], t);
for (int i: g[v]) {
if (i == fa[v] || i == son[v])continue;
dfs2(i, i);
}
}
/*线段树*/
namespace Segment_tree {
struct tree {
int l, r;
LL sum, lazy;
} tr[N * 4];
void push_up(tree &u, tree &l, tree &r) {
u.sum = l.sum + r.sum;
u.l = l.l, u.r = r.r;
}
void push_up(int u) {
push_up(tr[u], tr[u << 1], tr[u << 1 | 1]);
}
void build(int v, int l, int r) {
if (l == r) {
tr[v] = {l, l, nw[l], 0};
return;
}
int mid = l + r >> 1;
build(v << 1, l, mid);
build(v << 1 | 1, mid + 1, r);
push_up(v);
}
void push_down(int u) {
if (tr[u].lazy) {
auto &left = tr[u << 1], &right = tr[u << 1 | 1];
left.sum += tr[u].lazy * (left.r - left.l + 1);
right.sum += tr[u].lazy * (right.r - right.l + 1);
left.lazy += tr[u].lazy;
right.lazy += tr[u].lazy;
tr[u].lazy = 0;
}
}
void update(int u, int l, int r, int k) {
if (l <= tr[u].l && r >= tr[u].r) {
tr[u].lazy += k;
tr[u].sum += (tr[u].r - tr[u].l + 1) * k;
return;
}
push_down(u);
int mid = tr[u].l + tr[u].r >> 1;
if (l <= mid)update(u << 1, l, r, k);
if (r > mid)update(u << 1 | 1, l, r, k);
push_up(u);
}
LL query(int u, int l, int r) {
if (l <= tr[u].l && r >= tr[u].r)
return tr[u].sum;
push_down(u);
int mid = tr[u].l + tr[u].r >> 1;
LL res = 0;
if (l <= mid)res += query(u << 1, l, r);
if (r > mid)res += query(u << 1 | 1, l, r);
return res;
}
};
using namespace Segment_tree;
int lca(int u, int v) {
while (top[u] != top[v]) {
if (depth[top[u]] <= depth[top[v]])std::swap(v, u);
u = fa[top[u]];
}
return depth[u] < depth[v] ? u : v;
}
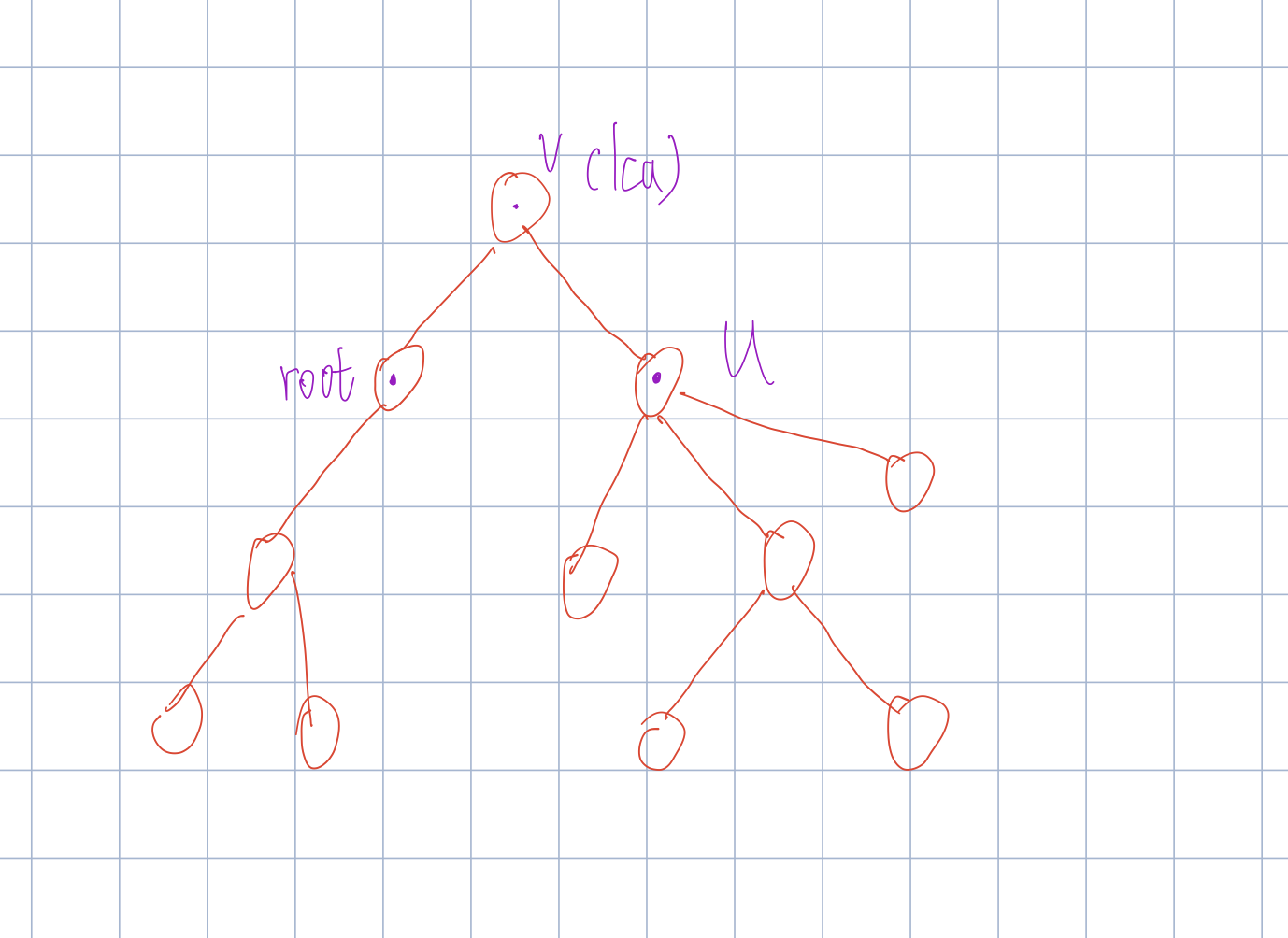
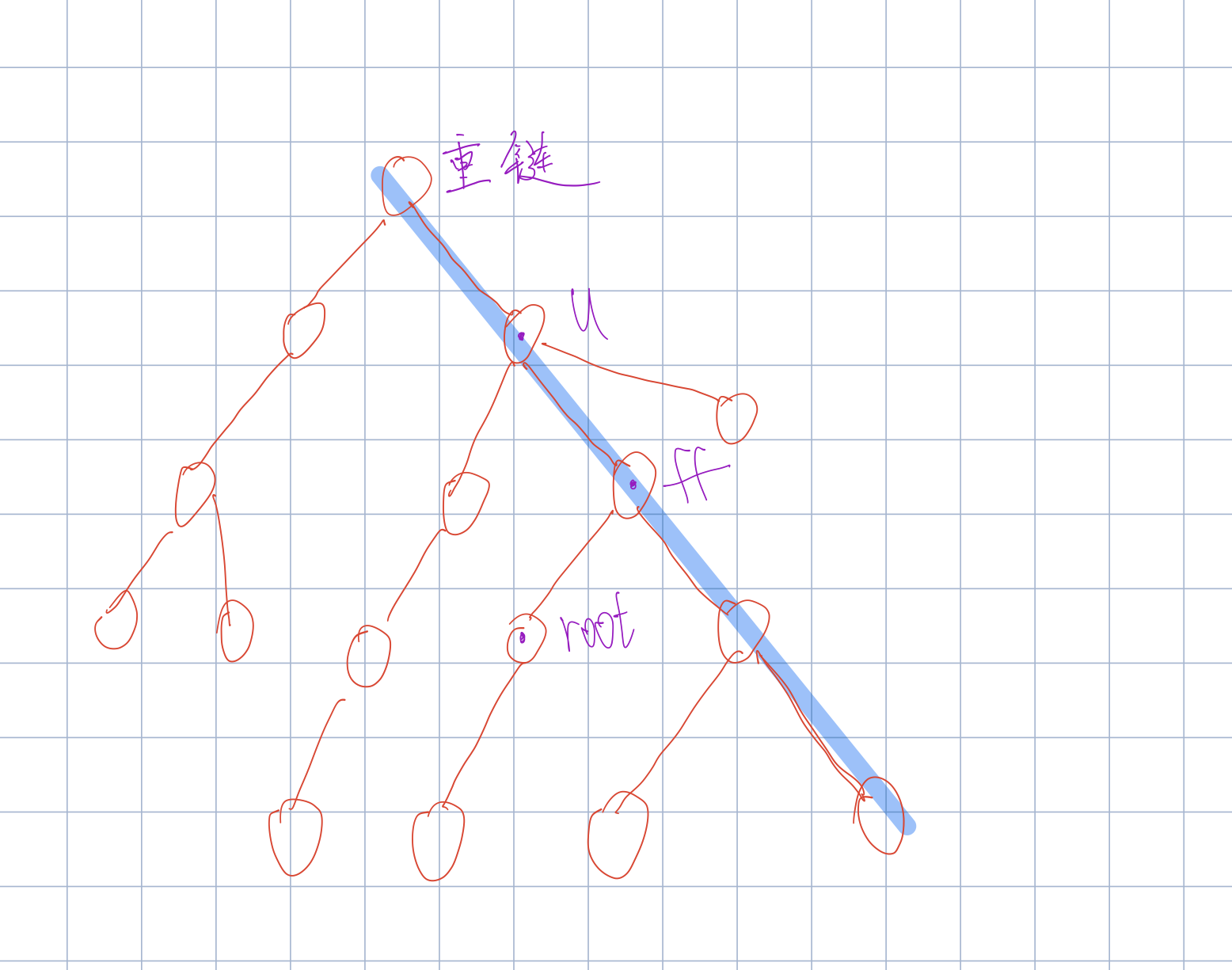
int find(int u,int v){//找到u到v路径上v的儿子
while(top[u]!=top[v]){//不在一个重链上
if(fa[top[u]]==v)return top[u];//如果u的重链顶点的父节点是v那直接返回重链顶点
u=fa[top[u]];//u到上一个重链上
}//因为v是u的公共祖先 所以 v一定在u的上面 不需要换位
//此时uv已在一根重链上 直接返回v的重儿子即可
return son[v];
}
void update_path(int u, int v, int k) {
while (top[u] != top[v]) {
if (depth[top[u]] < depth[top[v]])
std::swap(u, v);
update(1, id[top[u]], id[u], k);
u = fa[top[u]];
}
if (depth[u] < depth[v])std::swap(u, v);
update(1, id[v], id[u], k);
}
void update_tree(int u, int k) {
if(lca(root,u)!=u) update(1, id[u], id[u] + sz[u] - 1, k);
else {
int ff=find(root,u);
update(1,1,n,k);
if(u!=root)
update(1,id[ff],id[ff]+sz[ff]-1,-k);
}
}
LL query_tree(int u) {
if(lca(root,u)!=u) return query(1, id[u], id[u] + sz[u] - 1);
else {
if(root==u)return query(1,1,n);
int ff=find(root,u);
return query(1,1,n)-query(1,id[ff],id[ff]+sz[ff]-1);
// return ff;
}
}
LL query_path(int u, int v) {
LL res = 0;
while (top[u] != top[v]) {
if (depth[top[u]] < depth[top[v]])std::swap(u, v);
res += query(1, id[top[u]], id[u]);
u = fa[top[u]];
}
if (depth[u] < depth[v])std::swap(u, v);
res += query(1, id[v], id[u]);
return res;
}
signed main() {
std::ios::sync_with_stdio(false);
std::cin.tie(0);
std::cin >> n;
for (int i = 1; i <= n; i++)
std::cin >> in[i];
for (int i = 1; i < n; i++) {
int a;
std::cin>>a;
g[a].push_back(i+1);
g[i+1].push_back(a);
}
std::cin >> m;
dfs(1, 0);
dfs2(1, 1);
build(1, 1, cnt);
while (m--) {
int q, u, v, k;
std::cin >> q;
if (q == 1) {
std::cin >> root;
} else if (q == 2) {
std::cin >> u >> v >> k;
update_path(u, v, k);
} else if (q == 3) {
std::cin >> u >> k;
update_tree(u, k);
} else if (q == 4) {
std::cin >> u >> v;
std::cout << query_path(u, v) << "\n";
} else {
std::cin >> u;
std::cout << query_tree(u) << "\n";
}
}
return 0;
}
|